|
| Name | ArcByBulge |
|---|---|
| Type | gml:ArcByBulgeType |
| Nillable | no |
| Abstract | no |

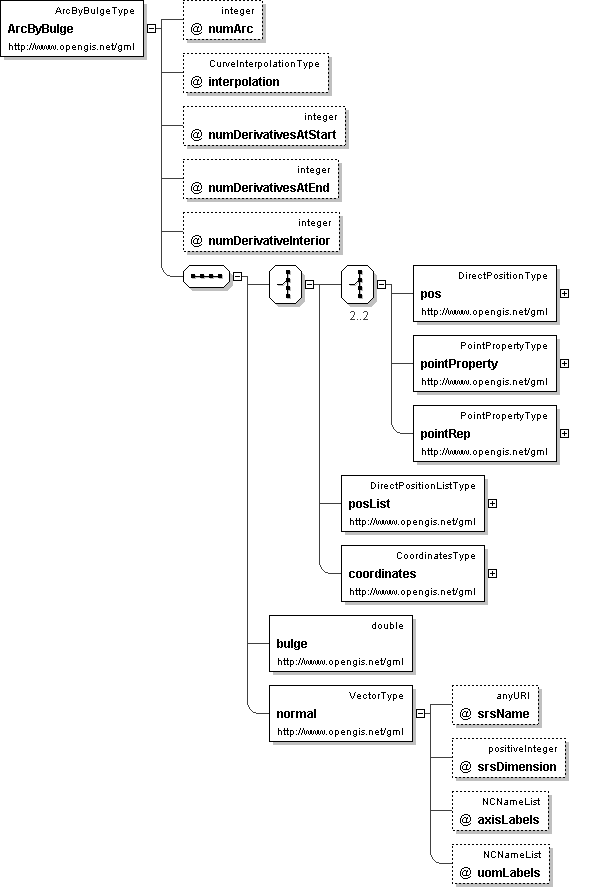
'The attribute \"numDerivativesAtStart\" specifies the type of continuity between this curve segment and its predecessor. If this is the first curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesAtEnd\" specifies the type of continuity between this curve segment and its successor. If this is the last curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesInterior\" specifies the type of continuity that is guaranteed interior to the curve. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
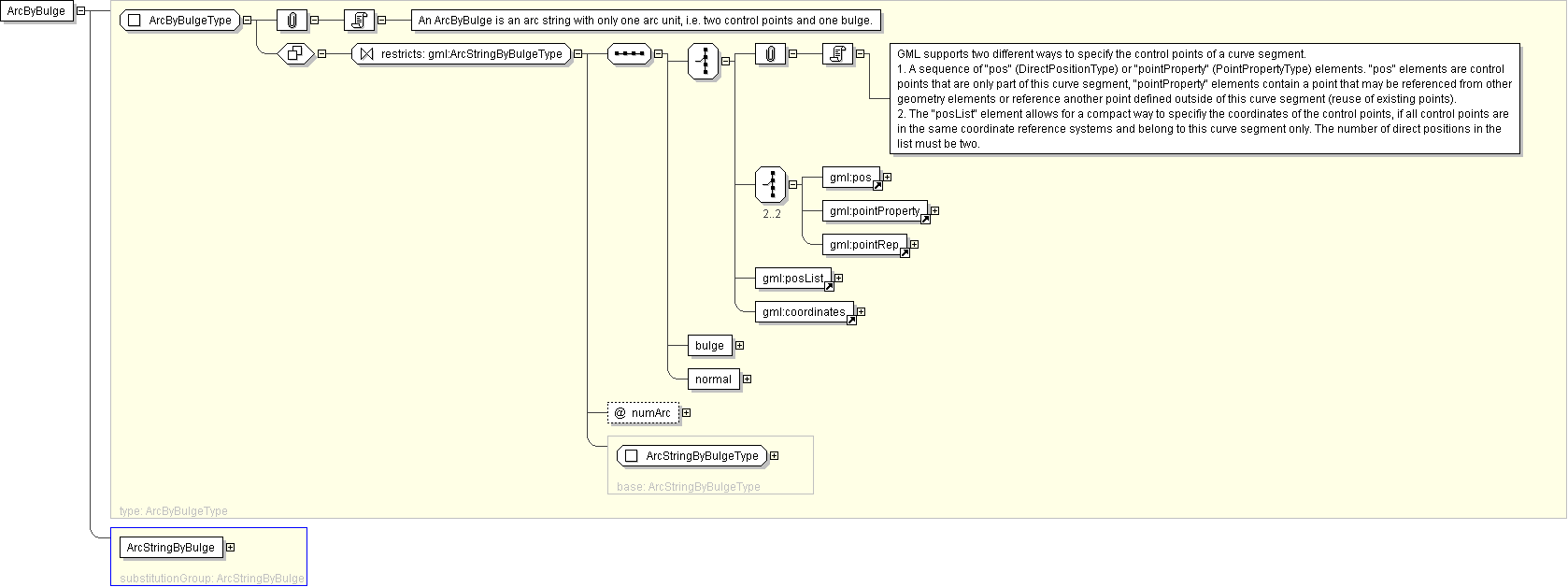
"'The attribute \"interpolation\" specifies the curve interpolation mechanism used for this segment. This mechanism uses the control points and control parameters to determine the position of this curve segment. For an ArcStringByBulge the interpolation is fixed as \"circularArc2PointWithBulge\".'
"'An arc is an arc string consiting of a single arc, the attribute is fixed to \"1\".'
">'GML supports two different ways to specify the control points of a curve segment. 1. A sequence of \"pos\" (DirectPositionType) or \"pointProperty\" (PointPropertyType) elements. \"pos\" elements are control points that are only part of this curve segment, \"pointProperty\" elements contain a point that may be referenced from other geometry elements or reference another point defined outside of this curve segment (reuse of existing points). 2. The \"posList\" element allows for a compact way to specifiy the coordinates of the control points, if all control points are in the same coordinate reference systems and belong to this curve segment only. The number of direct positions in the list must be two.'
'Deprecated with GML version 3.1.0. Use \"pointProperty\" instead. Included for backwards compatibility with GML 3.0.0.'
'Deprecated with GML version 3.1.0. Use \"posList\" instead.'
'The bulge controls the offset of each arc\'s midpoint. The \"bulge\" is the real number multiplier for the normal that determines the offset direction of the midpoint of each arc. The length of the bulge sequence is exactly 1 less than the length of the control point array, since a bulge is needed for each pair of adjacent points in the control point array. The bulge is not given by a distance, since it is simply a multiplier for the normal. The midpoint of the resulting arc is given by: midPoint = ((startPoint + endPoint)/2.0) + bulge*normal'
'The attribute \"normal\" is a vector normal (perpendicular) to the chord of the arc, the line joining the first and last point of the arc. In a 2D coordinate system, there are only two possible directions for the normal, and it is often given as a signed real, indicating its length, with a positive sign indicating a left turn angle from the chord line, and a negative sign indicating a right turn from the chord. In 3D, the normal determines the plane of the arc, along with the start and endPoint of the arc. The normal is usually a unit vector, but this is not absolutely necessary. If the normal is a zero vector, the geometric object becomes equivalent to the straight line between the two end points. The length of the normal sequence is exactly the same as for the bulge sequence, 1 less than the control point sequence length.'