| Super-types: | AbstractCurveSegmentType < GeodesicStringType (by extension) |
|---|---|
| Sub-types: |
|
| Name | GeodesicStringType |
|---|---|
| Abstract | no |
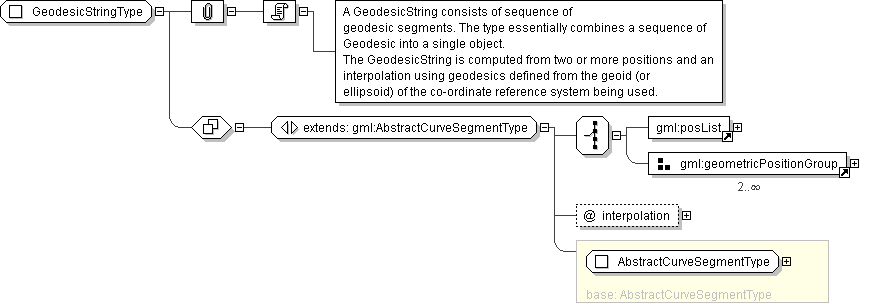
| Documentation | A GeodesicString consists of sequence of geodesic segments. The type essentially combines a sequence of Geodesic into a single object. The GeodesicString is computed from two or more positions and an interpolation using geodesics defined from the geoid (or ellipsoid) of the co-ordinate reference system being used. |
'The attribute \"numDerivativesAtStart\" specifies the type of continuity between this curve segment and its predecessor. If this is the first curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesAtEnd\" specifies the type of continuity between this curve segment and its successor. If this is the last curve segment in the curve, one of these values, as appropriate, is ignored. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"numDerivativesInterior\" specifies the type of continuity that is guaranteed interior to the curve. The default value of \"0\" means simple continuity, which is a mandatory minimum level of continuity. This level is referred to as \"C 0 \" in mathematical texts. A value of 1 means that the function and its first derivative are continuous at the appropriate end point: \"C 1 \" continuity. A value of \"n\" for any integer means the function and its first n derivatives are continuous: \"C n \" continuity. NOTE: Use of these values is only appropriate when the basic curve definition is an underdetermined system. For example, line string segments cannot support continuity above C 0 , since there is no spare control parameter to adjust the incoming angle at the end points of the segment. Spline functions on the other hand often have extra degrees of freedom on end segments that allow them to adjust the values of the derivatives to support C 1 or higher continuity.'
"'The attribute \"interpolation\" specifies the curve interpolation mechanism used for this segment. This mechanism uses the control points and control parameters to determine the position of this curve segment. For an GeodesicString the interpolation is fixed as \"geodesic\".'
">